За критику налоговой системы император заточил в темницу величайшего математика страны. Но однажды пленнику представился шанс вновь обрести свободу. Один из 12 наместников императора уплатил налог фальшивой монетой, которая уже попала в казну. Император пообещал освободить математика, если тот сумеет найти подделку.

Перед пленником поставили стол, на котором были чашечные весы, карандаш и 12 одинаковых на вид монет. А потом сказали, что фальшивка отличается от остальных денег по весу в большую или меньшую сторону. Взвесить монеты разрешили лишь трижды. Как математику вычислить подделку?
У математика всего три попытки, поэтому взвешивать каждую монету по отдельности нельзя. Нужно разделить их на кучки и класть на весы по несколько штук за раз, постепенно подбираясь к фальшивой.
Допустим, математик решил разделить 12 монет на три кучки по четыре монеты в каждой. Потом он положил на каждую чашу весов по четыре монеты. Такое взвешивание может дать два результата. Рассмотрим каждый из них.
1. Вес двух кучек с монетами оказался одинаковым. Следовательно, все деньги в них настоящие, а подделка лежит где‑то среди четырёх невзвешенных монет.
Чтобы отслеживать результат, математик помечает ноликом все подлинники. Потом берёт три из них и сравнивает с тремя невзвешенными монетами. Если их вес равен, то оставшаяся (четвёртая) невзвешенная монета фальшивая. Если вес отличается, то математик ставит на трёх непомеченных монетах плюс, если они тяжелее тех, что с ноликами, или минус, если они легче.
Потом он берёт две монеты, помеченные плюсом или минусом, и сравнивает их вес. Если он одинаковый, то оставшийся экземпляр — подделка. Если нет, математик смотрит на знаки: среди монет с плюсом фальшивой будет та, что тяжелее, среди монет с минусом — та, что легче.
2. Вес двух кучек с монетами оказался неодинаковым.
В этом случае математику нужно действовать так: пометить деньги в тяжёлой кучке плюсом, в лёгкой — минусом, в невзвешенной — ноликом, так как известно, что фальшивый экземпляр был на весах.
Теперь нужно перегруппировать монеты, чтобы уложиться в два оставшихся взвешивания. Один из способов — взять вместо трёх монет с плюсом три монеты с минусом, а на их место положить три штуки с ноликом.
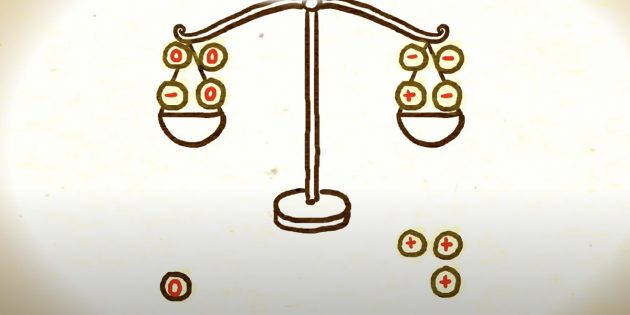
Далее следует три возможных варианта. Если та чаша весов, которая была тяжелее, всё ещё перевешивает, значит, либо старая монета со знаком плюс на ней тяжелее остальных, либо оставшаяся на другой чаше весов монета со знаком минус — легче. Математику нужно выбрать любую из них и сравнить с обычным образцом, чтобы найти фальшивку.
Если же та чаша весов, которая была тяжелее, стала легче, значит, одна из трёх перемещённых математиком монет со знаком минус и есть самая лёгкая. Теперь ему нужно сравнить на весах две из них. При равенстве результатов третья монета будет поддельной. При неравенстве — фальшивая та, что легче.
Если после замены чаши уравновесились, одна из трёх снятых с весов монет со знаком плюс тяжелее остальных. Математику нужно сравнить две из них. При их равенстве третья — поддельная. При неравенстве ненастоящая та, что тяжелее.
Император одобрительно кивает, выслушивая рассуждения математика, а нечестный наместник отправляется в темницу.
Эта загадка — перевод видео TED‑Ed.