1. Мудрый мельник
Мельник показал своим знакомым 9 мешков с зерном, которые стояли, как показано на рисунке, и сказал:
— Я загадаю вам загадку про эти мешки пшеницы. Заметьте, что по бокам стоит по 1 мешку, затем идут пары мешков, а посредине вы видите 3 мешка. Если умножить левую пару 28 на левый мешок 7, то получится 196, что и указано на средних мешках. Но если вы умножите правую пару 34 на правый мешок 5, то не получите при этом 196. Задача состоит в следующем: переставить эти 9 мешков так, чтобы каждая пара, умноженная на своего соседа, давала число, стоящее в середине.

Нужно разместить мешки следующим образом: 2, 78, 156, 39, 4. Здесь каждая пара, умноженная на соседний мешок, даёт число, стоящее в середине. При этом пришлось передвинуть пять мешков.
Существует ещё три варианта расположения мешков: 4, 39, 156, 78, 2, или 3, 58, 174, 29, 6, или 6, 29, 174, 58, 3, но при этом потребовалось бы передвинуть семь мешков.
2. Сколько картофелин?
Шли 3 крестьянина и зашли на постоялый двор отдохнуть и пообедать. Заказали хозяйке сварить картофель, а сами заснули. Хозяйка сварила картофель, но не стала будить постояльцев, а поставила миску с едой на стол и ушла.
Проснулся один крестьянин, увидел картофель и, чтобы не будить товарищей, сосчитал картофель, съел свою долю и снова заснул. Вскоре проснулся другой; он не знал, что один из товарищей уже съел свою долю, поэтому он сосчитал весь оставшийся картофель, съел третью часть и опять заснул. После него проснулся третий; полагая, что он проснулся первым, он сосчитал оставшийся в миске картофель и съел третью часть.
Тут проснулись его товарищи и увидели, что в миске осталось 8 картофелин. Тогда они всё поняли. Сосчитайте, сколько картофелин подала на стол хозяйка, сколько съел уже и сколько должен съесть ещё каждый, чтобы всем досталось поровну.
Третий крестьянин оставил для товарищей 8 картофелин, то есть каждому по 4 штуки. Значит, и сам он съел четыре картофелины. После этого легко сообразить, что второй крестьянин оставил своим товарищам 12 картофелин, по 6 на каждого, значит, и сам съел 6 штук. Отсюда следует, что первый крестьянин оставил товарищам 18 картофелин, по 9 штук на каждого, значит, и сам съел 9 штук.
Итак, хозяйка подала на стол 27 картофелин, и на долю каждого поэтому приходилось по 9 картофелин. Но первый крестьянин всю свою долю съел. Следовательно, из оставшихся 8 картофелин приходится на долю второго 3, а на долю третьего — 5 штук.
3. Цифры в круг
Цифры от 1 до 9 надо разместить в фигуре на рисунке так, чтобы 1 цифра была в центре круга, прочие — у концов каждого диаметра и чтобы сумма 3 цифр каждого ряда при этом составляла 15.
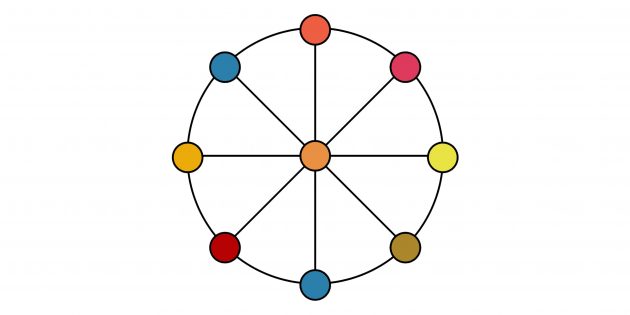
Ответ представлен на рисунке.
4. Варка яиц
Как проще всего отмерить 15 минут, необходимые для варки яиц, имея под рукой семи- и одиннадцатиминутные песочные часы?
Приведём 2 возможных решения. Первое из них является оптимальным с точки зрения продолжительности всех операций, второе — с точки зрения того, сколько раз приходится переворачивать часы.
1. Положив яйцо в воду, пустите одновременно семи- и одиннадцатиминутые часы. По истечении 7 минут переверните семиминутные часы в первый, а по истечении 11 минут (когда весь песок из верхней половины одиннадцатиминутных часов пересыплется в нижнюю половину) — во второй раз. Песок перестанет пересыпаться из верхней половины семиминутных часов в нижнюю как раз к концу пятнадцатой минуты.
2. Перевернув одновременно семи- и одиннадцатиминутные часы, начинаем отсчёт времени. После того как верхняя половина семиминутных часов опустеет, кладём яйцо в воду. Дождавшись, когда весь песок из верхней половины одиннадцатиминутных часов пересыплется в нижнюю, переворачиваем их. Когда верхняя половина одиннадцатиминутных часов снова опустеет, с момента начала варки яиц пройдёт ровно 15 минут.
5. Родня
Нанимая нового работника, спросили, большая ли у него семья, тот ответил:
— У меня братьев и сестёр поровну, но вот у моей сестры братьев вдвое больше, чем сестёр.
Никто так и не смог подсчитать, сколько детей в семье нового работника. Может быть, вам это удастся?
В семье нового работника всего семеро детей. Четверо из них мальчики и трое — девочки. Поэтому у каждого мальчика по 3 брата и по 3 сестры, а у каждой девочки по 4 брата и по 2 сестры.
6. Хорошая пара
— Сколько лет Иванову?
— Давайте сообразим. 18 лет назад, в год своей женитьбы, он был, я помню, ровно втрое старше своей жены.
— Позвольте, насколько мне известно, он теперь как раз вдвое старше своей жены. Это другая жена?
— Та же. И потому нетрудно установить, сколько сейчас лет Иванову и его жене.
Так сколько же?
Если жене теперь х лет, то мужу — 2х. 18 лет назад каждому их них было на 18 лет меньше: мужу — (2х − 18), жене — (х − 18). При этом известно, что муж тогда был старше жены: 3(х − 18) = 2х − 18. Решим уравнение: 3х − 54 = 2х — 18. 3х − 2х = 54 − 18. х = 36. 2х = 72. Жене теперь 36, мужу — 72.
7. Два кофейника
Есть 2 кофейника одинаковой ширины: один высокий, другой низкий. Какой из них вместительнее?

Многие, вероятно, не подумав, скажут, что высокий кофейник вместительнее низкого. Если бы вы, однако, стали лить жидкость в высокий кофейник, вы смогли бы налить в него только до уровня отверстия его носика — дальше вода начнёт выливаться. А так как отверстия носика у обоих кофейников на одной высоте, то низкий кофейник оказывается столь же вместительным, как и высокий.
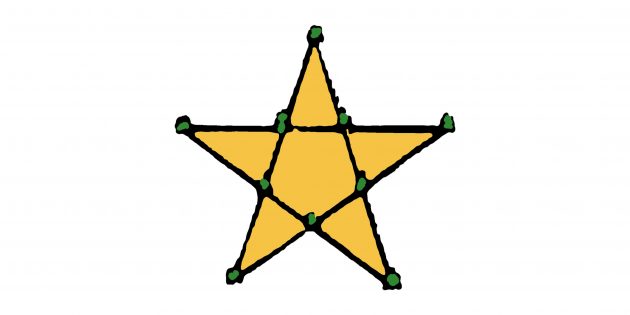
8. Недогадливый садовник
Однажды хозяин поручил садовнику посадить 10 деревьев. При этом он потребовал разместить их таким образом, чтобы получилось 5 рядов и в каждом ряду по 4 дерева. Только благодаря помощи странствующего мудреца садовнику удалось выполнить распоряжение хозяина. А как бы вы разместили деревья?
Садовнику необходимо было разместить посадку в форме пятилучевой звезды. При этом деревья следовало сажать в точках пересечения линий звезды, как это показано на рисунке.
9. Шесть пароходов
По каналу, один за другим, идут 3 парохода: А, Б, В. Навстречу им показались ещё 3 парохода, которые тоже идут один за другим: Г, Д, Е. Канал такой ширины, что 2 парохода разъехаться не могут, но в канале с одной стороны есть залив, в котором может поместиться только 1 пароход.
Могут ли пароходы разъехаться так, чтобы продолжать свой путь по‑прежнему?
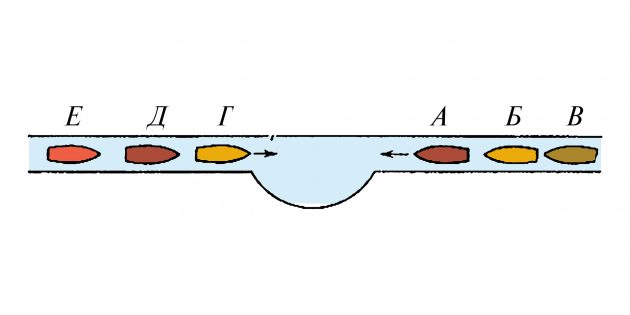
Пароходы Б и В отходят назад (вправо), А входит в залив; Г, Д и Е проходят по каналу мимо А; тогда А выходит из залива и идёт своей дорогой (влево). Е, Д и Г отступают на прежнее место (налево); тогда с Б повторяется всё, что делалось с А. Таким же образом проходит и В, и пароходы плывут своей дорогой.
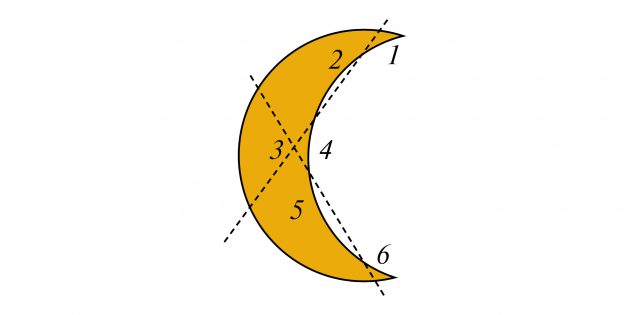
10. Поделите луну
Фигуру лунного серпа требуется разделить на 6 частей, проведя только 2 прямые линии. Как это сделать?

Сделать надо так, как показано на рисунке. Получается 6 частей, которые для наглядности пронумерованы.
11. И ещё одно яблочко
Есть корзина с 5 яблоками. Как разделить их между 5 людьми так, чтобы каждый из них получил по 1 яблоку и ещё 1 яблоко осталось в корзине?
4 человека берут из корзины по одному яблоку, а пятый берёт яблоко вместе с корзиной.
12. До заводских ворот
Двое рабочих, старик и молодой, живут в одной квартире и работают на одном заводе. Молодой доходит до завода за 20 минут, старый — за 30 минут. Через сколько минут молодой догонит старого, если последний выйдет из дому пятью минутами раньше него?
На прохождение всего пути старый рабочий тратит на 10 минут больше молодого. Выйди старик на 10 минут раньше молодого, оба пришли бы на завод в одно время. Если старик вышел только на 5 минут раньше, то молодой должен нагнать его как раз посередине пути, то есть спустя 10 минут (весь путь молодой рабочий проходит за 20 минут).

Все эти загадки взяты из книги «Лучшие советские задачи и головоломки» И. Е. Гусева и А. Г. Мерникова. Проверенные временем задачки помогут отвлечься от гаджетов и потренировать логическое мышление.
Сколько головоломок вам удалось разгадать без подсказок? Делитесь в комментариях!