В 5 раз? Серьёзно?
«Гослото „7 из 49“» — это всероссийская государственная лотерея. Организатор — Министерство спорта РФ. Правила простые: чтобы участвовать в розыгрыше, надо отметить минимум 7 из 49 чисел в билете.
Раньше надо было угадать хотя бы три числа, выпавших во время розыгрыша. За это участники получали 125 рублей. Теперь в лотерее появилась новая категория: угадываете два числа — получаете 200 рублей.
С новыми правилами вероятность выигрыша увеличилась с 1 к 19,8 до 1 к 3,9. Это значит, что 25% билетов счастливые: деньги может принести каждый четвёртый. А раз вырос шанс, то и билет теперь стоит 200 рублей.
Счастливчикам, у которых совпали все семь чисел, достаётся суперприз.
Сумма суперприза — 500 000 000 рублей!
Пока что самый большой выигрыш в истории «Гослото „7 из 49“» — 134 957 197 рублей. 17 сентября 2018 года его получил пенсионер из Красноярска.
Звучит слишком хорошо. Считаем шансы на победу
С помощью гипергеометрического распределения мы можем проверить, действительно ли вероятность выигрыша может быть почти 25%, или 1 к 3,9.
Помните, был анекдот про мужика, который в изолированной комнате один металлический шарик потерял, а другой сломал? Вот сейчас мы поговорим примерно про это.
Похитили марсиане американца, француза и русского и говорят: «Мы посадим каждого из вас в одиночную камеру, дадим каждому по два титановых шарика и по часу времени. Кто из вас больше всех нас удивит, того мы отпустим, предварительно наделив космической энергией. А остальных отправим на опыты».
Спустя час заходят марсиане к американцу. Тот шариками жонглирует. Марсиане: «Хорошо, удивил, молодец». Заходят к французу — тоже шариками жонглирует, но с закрытыми глазами и стоя на голове лицом к стенке. Марсиане: «Супер! Ты лучший! Можно к русскому и не заходить, но раз обещали…». Выходят от русского: «Американца и француза на опыты — русский один шарик сломал, а второй потерял».
Так вот гипергеометрическое распределение возникает естественным образом в такой жизненной ситуации: у вас есть мешок с шариками. Некоторые из них были сломаны русским из того анекдота. Вы берёте случайную горсть шариков из мешка, но стесняетесь посмотреть, какие именно вытащили. И думаете: «Интересно, какая вероятность того, что в руке один, два или три сломанных шарика?»
Гипергеометрическое распределение — это такая «база данных» для вероятностей того, что у вас в руке сейчас. Оно описывает вероятности всех возможных исходов: вероятность, что в руке 0 сломанных шариков, 1 сломанный шарик, 2 и так далее.
Но как это связано с лотереей?
Очень просто:
- Мешок с шариками — это все возможные числа в билете от 1 до 49;
- Сломанные шарики — те выигрышные числа, которые при розыгрыше определяет лототрон;
- А горсть — числа, отмеченные в билете игрока.
Если применить формулу расчета вероятностей для гипергеометрического распределения к новым правилам лотереи «Гослото „7 из 49“», можно узнать примерные шансы на победу с определённым счётом. И получится 1 к 3,9.
А вот и формула расчёта вероятностей для гипергеометрического распределения:
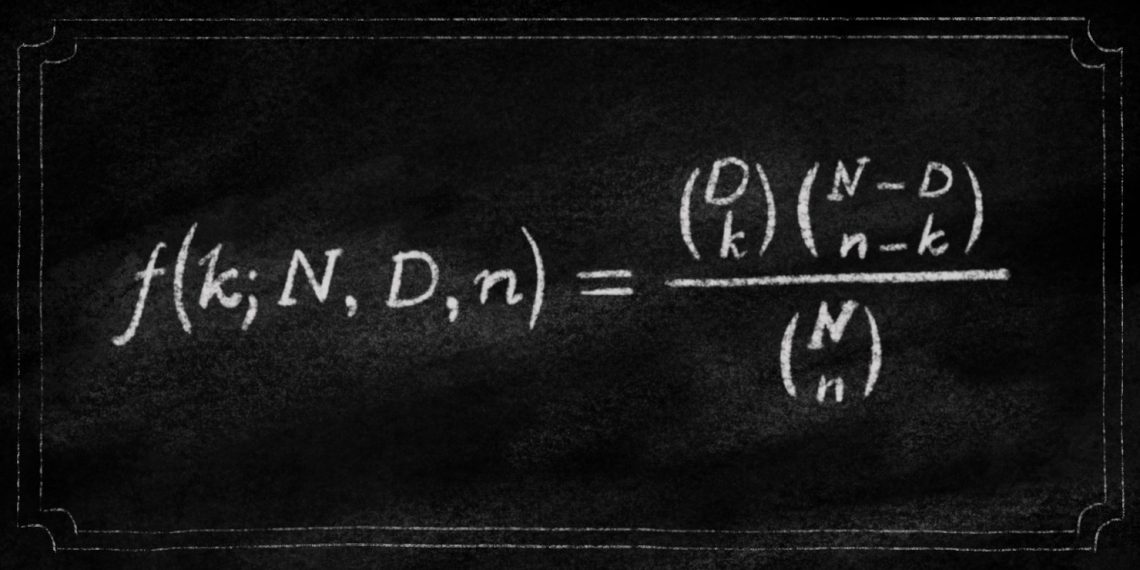
D — количество выигрышных чисел,
N — количество чисел в лотерее всего,
n — количество выбранных игроком чисел в билете,
k — размер выигрышной комбинации.
Как всё это понимать? Что это за скобки?
Предположим, что у нас есть лотерея, где всего 4 возможных числа, из которых можно вычеркнуть только 2 в билете. Выбрать эти числа можно как-то так:

Каждый столбец — это возможное сочетание. Всего получается 6 вариантов. Это называется число сочетаний из 4 по 2. Хитрые люди придумали, как его посчитать для произвольного количества чисел в лотерее и количества чисел, которое можно вычеркнуть в билете. Решили, что записывать будут так:
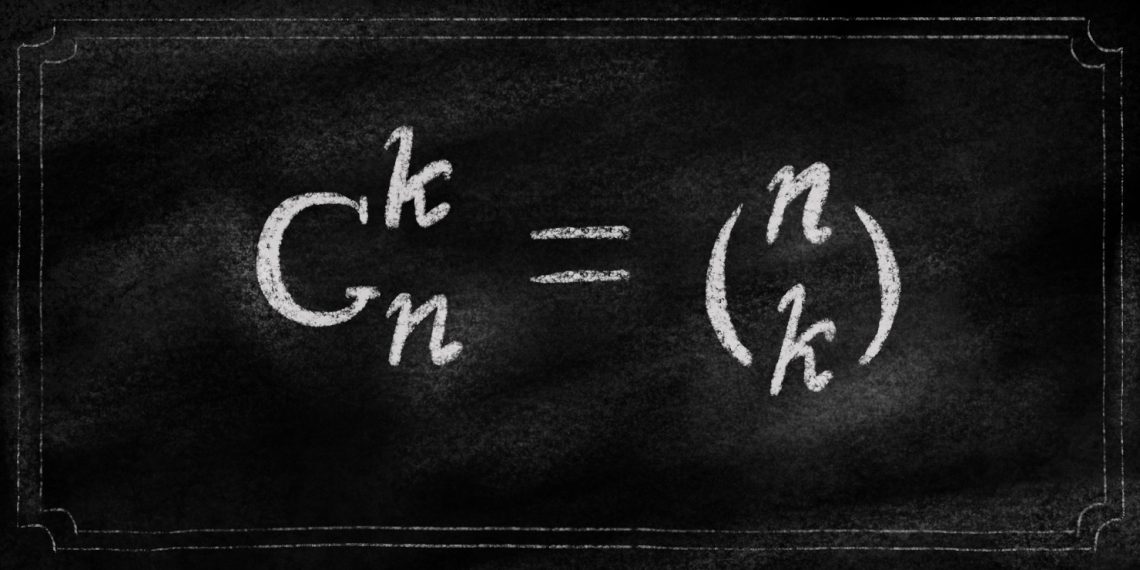
Мы же будем это записывать как C(n,k). В нашем случае — C(4,2) = 6. Как раз те самые скобочки из формулы вероятностей для гипергеометрического распределения. Теперь самое время взглянуть на неё новыми глазами. Она запишется у нас в таком виде:
f(k,N,D,n) = C(D,k)*C(N-D,n-k)/C(N,n)
Можно считать:
C(N,n) — например, у игрока билет с числами (1,2,3,4,5,6,7). Это только одно из возможных сочетаний из 49 чисел в лотерее. И таких сочетаний всего теоретически может быть C(N,n) = C(49,7). То есть это число показывает, сколько разных выигрышных комбинаций всего может быть в лотерее.
C(D,k) — например, выигрышная комбинация из 7 чисел — (1,4,7,12,55,44,33). И мы смотрим на все возможные сочетания пар — (1,4), (1,55), (12,33)… Этих сочетаний теоретически возможно всего C (D,k) = C(7,2). Пока просто запомним.
C(N-D,n-k) — самое интересное. К примеру, у нас есть выигрышная пара (1,4). Тогда все остальные числа могут быть какими угодно, только не выигрышными. Например, (1,4,3,2,5,6,8). Мы должны посчитать, каким количеством способов мы можем выбрать оставшиеся 5 чисел из тех 42, которые гарантировано проиграли. В нашем случае это C(N-D,n-k) = C(49-7,7-2).
Так мы посчитали все сочетания только для одной из выигрышных комбинаций. Но надо-то для всех. Поэтому, чтобы получить общее количество выигрышных комбинаций, мы умножаем друг на друга C(D,k) и C(N-D,n-k).
А дальше просто. Делим выигрышные сочетания на все теоретически возможные, чтобы получить вероятность выиграть с выигрышной комбинацией размера k. В данном примере это k = 2, но может быть 3, 4, 5… Осталось просто посчитать для всех выигрышных комбинаций лотереи:
Для k = 2: f(2,49,7,7) = C(7,2)*C(49-7,7-2)/C(49,7) = 0,2080
Для k = 3: f(3,49,7,7) = C(7,3)*C(49-7,7-3)/C(49,7) = 0,0456
Для k = 4: f(4,49,7,7) = C(7,4)*C(49-7,7-4)/C(49,7) = 0,0047
Дальше можно не считать, потому что вероятность слишком мала. Так что складываем все эти вероятности и получаем f([2,3,4],49,7,7) = 0,2583. А теперь момент истины. Берём заявленный показатель 1/3,9, производим деление и получаем 0,2564 – число, близкое вероятности 0,2583. Что ж, заявление «Столото» похоже на правду!
Проверяем, как на самом деле работает «Гослото „7 из 49“»
Участвовать в лотерее мы решили с помощью мобильного приложения «Столото». Оно работает на iOS и Android. Здесь удобно покупать билеты, выбирать комбинации чисел и следить за ходом розыгрыша, а когда он закончится, «Столото» пришлёт уведомление о результатах тиража. Кроме приложения, можно попытать счастья онлайн на сайте «Столото» или приобрести бумажный купон.
Итак, раз обещают, что выиграть может каждый четвёртый билет, мы решили, что будем брать столько билетов, чтобы их количество было кратно четырём. Исключение сделали только для первого розыгрыша: пока присматривались к лотерее, купили один билет за 200 рублей на ближайший тираж.
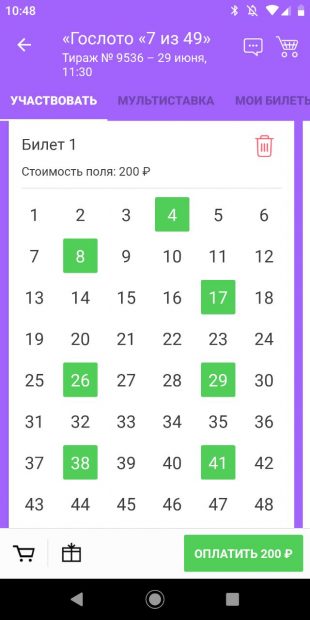
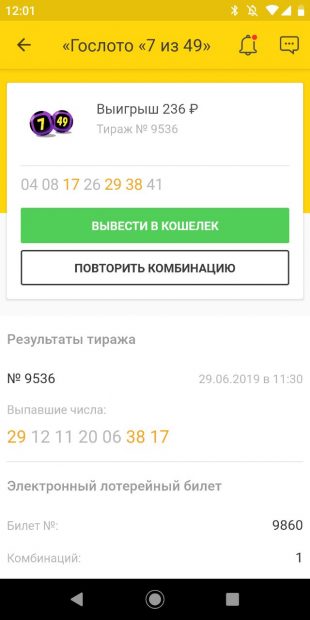
В нём совпало три числа. Чтобы не тратить деньги зря и проверить лотерею со всех сторон, дальше мы играли в три захода.
Четыре билета на один тираж
В мобильном приложении «Столото» можно заполнить билеты вручную или выбрать комбинацию автоматически. Владельцам iPhone для этого надо просто потрясти смартфон.
Идём по плану: покупаем 4 билета и в каждом отмечаем по 7 чисел.
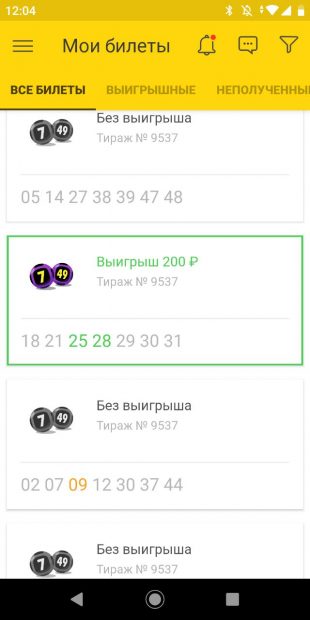
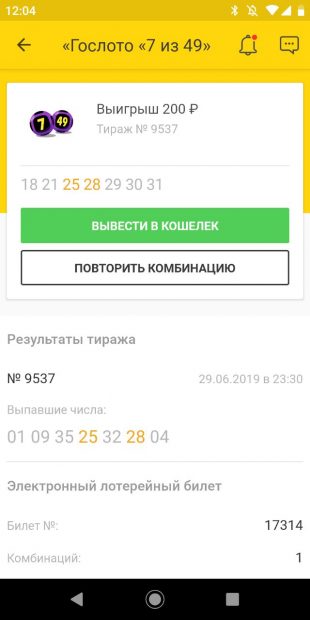
Один билет оказался выигрышным: два совпавших числа. Неплохо, но выводы делать пока рано.
Мультиставка
В разделе «Мультиставка» можно приобрести до 100 билетов на 5 ближайших тиражей. У такого подхода есть два преимущества:
- Вы экономите время. Не нужно по отдельности покупать билеты для каждого розыгрыша и вручную отмечать комбинации чисел.
- Повышаются шансы на победу. Чем больше билетов участвуют в тираже, тем больше количество потенциально выигрышных комбинаций.
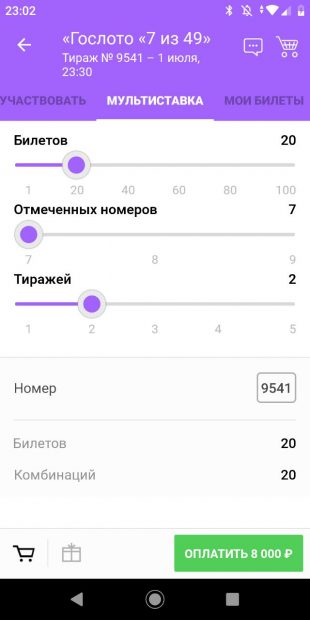
С мультиставкой мы экспериментировали дважды. Сначала взяли 12 билетов на два тиража.
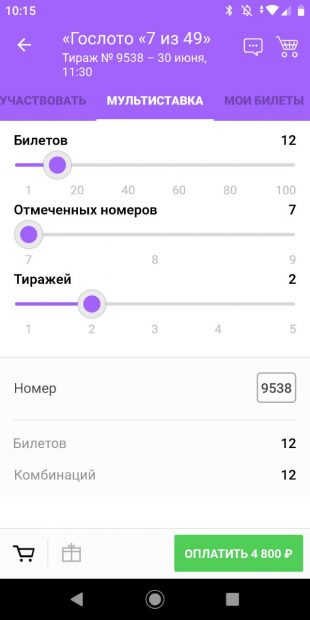
Удачными оказались три билета, а это те самые 25% из пачки. Причём одному повезло в обоих тиражах.
Чтобы закрепить результат, мы решили ещё раз поучаствовать в лотерее с мультиставкой и на два тиража набрали 20 билетов.
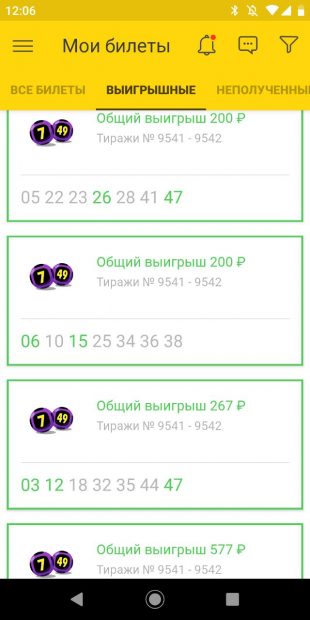
Вот здесь уже интереснее: 9 из них стали счастливыми, а два выиграли в обоих тиражах.
Развёрнутая ставка
В билете можно отметить не 7 чисел, а больше: до 12 в мобильном приложении, 12 — на сайте и 16 в бумажном купоне. Это называется развёрнутой ставкой, и она увеличивает шансы на выигрыш. Количество комбинаций растёт, а значит, повышается вероятность, что отмеченные номера совпадут с выпавшими во время розыгрыша. Билет в таком случае становится дороже: если отметить 8 чисел, придётся заплатить за него не 200, а 1 600 рублей.
Можно сочетать разные тактики и покупать на один тираж билеты с развёрнутой ставкой и те, в которых отмечено 7 чисел. Мы не стали мелочиться, взяли 4 билета и автоматически отметили по 8 чисел в каждом.
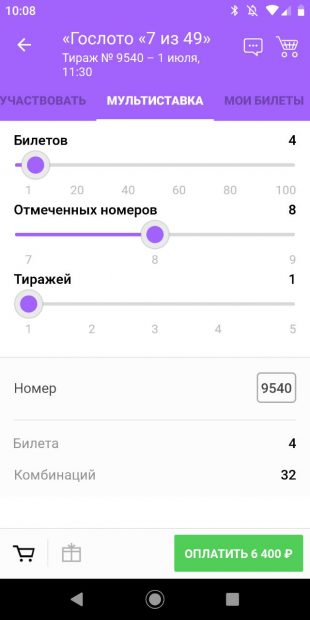
32 возможные комбинации — это серьёзная заявка на успех, но что-то пошло не так. Ни в одном из четырёх билетов не совпало больше одного числа.
Итоги
Всего мы купили 41 билет:
- 1 билет на 1 тираж — совпало 2 номера. Приятно, но не очень показательно.
- 4 билета на 1 тираж — выиграл 1 билет. Ровно то, что и говорили организаторы.
- 32 билета с мультиставкой — 12 из них оказались счастливыми. Статистика не подвела: на этом этапе примерно 38% билетов принесли выигрыш.
- 4 билета с развёрнутой ставкой — выигрышных среди них не оказалось.
По результатам наших опытов вероятность выиграть оказалась даже выше обещанного. Выстрелили 14 билетов из 41, а это примерно 34% против обещанных 25%.
Однако всё дело в тактике. На нашей стороне были и новые правила, и условия участия в лотерее с мультиставкой. Мы покупали не только по одному билету на тираж, но и брали сразу партию, где количество билетов кратно четырём, на несколько тиражей.
Чаще всего наши билеты выигрывали в той самой категории, где нужно угадать всего два числа из семи. Если перевести эту вероятность в проценты, получается около 25%. Эксперимент можно считать успешным: похоже, что с новыми правилами получить выигрыш стало проще.
Испытать удачу