Какого числа не хватает? 10 интересных заданий на поиск закономерностей

9. Цифры в столбцах складываются в трёхзначные числа, каждое из которых является кубом чисел 7, 8, 9. 7³ = 343; 8³ = 512; 9³ = 729.

1. Сумма чисел в каждой строке, каждом столбце и на обеих диагоналях равна 15. Значит, вместо знака вопроса нужно подставить 15 − (9 + 5) = 1.

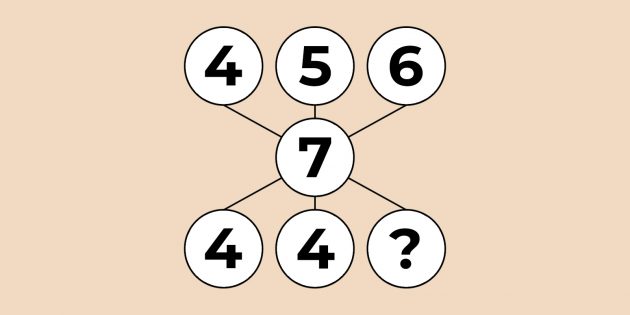
9. Число в нижнем ряду равно 456 − 7 = 449.

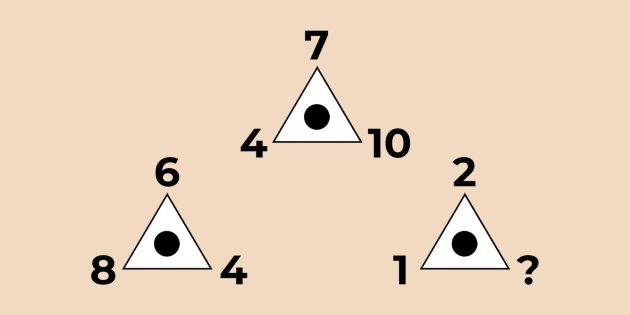
3. Число, расположенное на вершине каждого треугольника, — это среднее арифметическое двух чисел, расположенных в его основании.

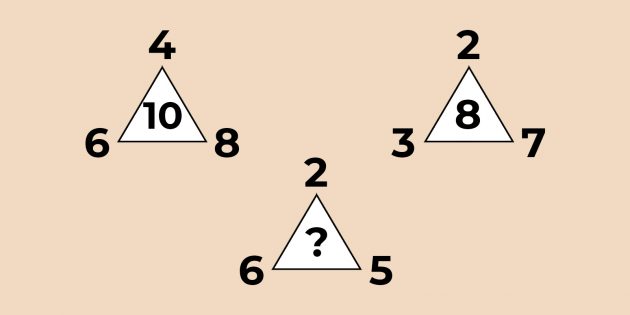
9. Чтобы найти число в центре треугольника, нужно от левого числа в его основании отнять число в его вершине, а потом прибавить правое число в его основании. 6 − 4 + 8 = 10; 3 − 2 + 7 = 8; 6 − 2 + 5 = 9.

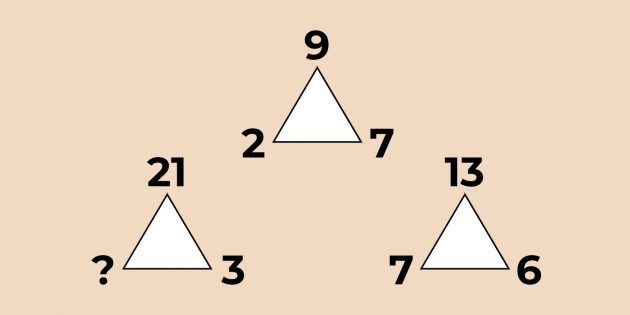
18. Сумма двух чисел в основании равна числу на вершине. Значит, в нижнем левом треугольнике не хватает числа 21 − 3 = 18.

22. Продвигаясь слева направо, складываем 3 и 6, потом отнимаем 4. Повторяем для каждой пары. 11 + 15 − 4 = 21.

7. Нижний ряд чисел получается суммированием верхнего и среднего и прибавлением 2. 4 + 1 + 2 = 7.

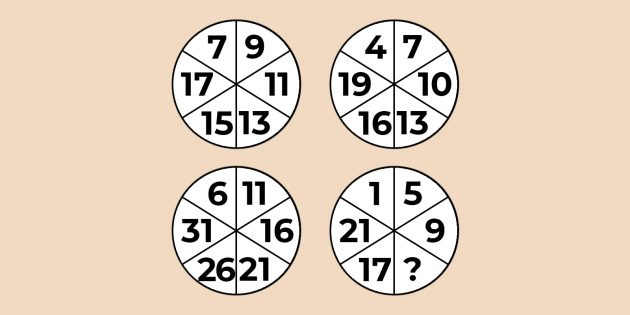
13. Если рассматривать круги с числами, начиная с левого верхнего и перемещаясь по часовой стрелке, можно заметить, что в первом круге числа увеличиваются на 2, начиная с числа 7, во втором круге — на 3, начиная с числа 4, в третьем — на 4, начиная с числа 1, в четвёртом — на 5, начиная с числа 6. Значит, в третьем круге не хватает числа 9 + 4 = 13.

4. Чтобы найти числа, расположенные в левом нижнем сегменте каждого круга, нужно сложить числа двух верхних сегментов. Например: 7 + 2 = 9. Чтобы найти числа, расположенные в нижнем правом сегменте каждого круга, нужно вычесть числа двух верхних сегментов. Например: 7 − 2 = 5. Значит, в правом нижнем кругу не хватает 11 − 7 = 4.